Financial mathematics is the most important application of mathematics for the finance professionals. It includes various topics such as Time value of money, evaluation of cash flow, calculation of current yields and YTM (Yield to Maturity), bond pricing and estimation of volatility.
Time value of money concepts and formulas are useful to supervisory level staff members in banks, insurance companies, financial institutions, brokerage houses, mutual funds etc. Derivation of formulas is not in the scope of this article and hence we have directly provided the formulas for your reference.
Recap of few basic concepts of finance in the context of time value of money
1. What is compounding?
Compounding is the process of investing and reinvesting the principal amount along with the interest earned thereon. It is applicable in the context of future value calculation.
2. What is discounting?
Discounting is the inverse of compounding. It is applicable in the context of present value calculation.
3. What is an annuity?
Annuity is a stream of constant cash flow (payments or receipts) occurring at regular intervals of time.
4. What is a deferred annuity?
Deferred annuity or regular annuity or ordinary annuity refers to cash flows occurring at the end of each period.
5. What is annuity due?
Annuity Due means the cash flows occur at the beginning of each period.
6. What is a growing annuity?
If the cash flow grows at the constant rate, then it is termed as Growing Annuity.
7. What is perpetuity?
Perpetuity is an annuity of infinite duration.
Applications of Time Value of Money
Applications of Future Value Concept
- Calculation of maturity amount of bank deposits
- Estimating doubling period of any investment for a given interest rate
- Calculation of growth rate
Application of present value concept
If someone asks you as a bank officer that he/she wants Rs.1,00,000 after 10 years for children’s education, how much amount he/she should invest now in a term deposit. You can work out present value presuming say 10% discounting factor and recommend accordingly.
Application of future value of an annuity
- Calculation of maturity amount in a recurring deposit account with a fixed sum invested every month for a fixed period with a known interest rate.
- Calculation of maturity amount in a SIP (Systematic investment plan) of mutual fund with a fixed sum invested every month for a fixed period presuming a certain rate of return.
- Calculation of maturity amount in a public provident fund account with a fixed sum invested every year for 15 years.
- Calculation of how much amount you need to invest every year to buy a house worth certain amount after ten years presuming certain rate of return on your investment.
Application of present value of an annuity
- You can calculate how much you can borrow for a car based on your budget amount towards monthly repayment of loan.
- You can determine loan amortization schedule.
- You can work out period of loan repayment from various known parameters.
Application of present value of a growing annuity
Example – You wish to buy a property for leasing it to some company for a period of next 10 years. Company has promised yearly rent of Rs.100,000 for the first year and thereafter the rent would increase at the rate of 10% per year. You can presume a reasonable rate of discounting for the next 10 years – say 12%. Now you can find out how much amount you need to allocate for buying the property by using the formula for present value of a growing annuity. Likewise, you can find out how much lumpsum amount you need to invest now in a pension plan that would provide you an increasing amount of pension every year.
Application of intra-year compounding
Formulas for FV and PV take into account annual compounding. However, in many cases compounding is quarterly – for example in term deposits of banks. In such cases, the formulas for FV and PV need modifications for intra-year compounding effect. Frequency of compounding = 4 in quarterly compounding; Frequency of compounding = 2 in half yearly compounding.
Application of effective versus stated rate
A public sector bank offers you 12% interest rate on its term deposit for a period of five year. You can find out what would be the effective rate of interest if compounding were done quarterly. Here in this case, the stated rate is 12% per annum but with quarterly compounding, the effective interest rate works out to 12.55%
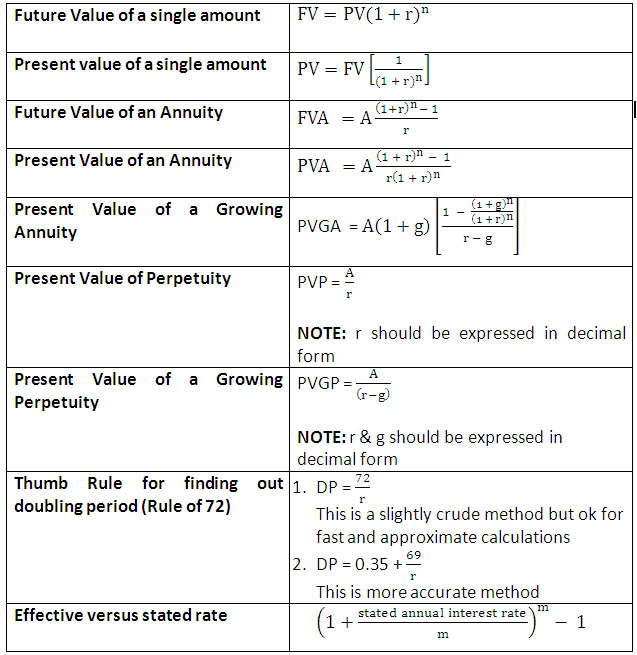
Time Value of Money Formulas
Legend:
- r = Interest rate or compunding rate or discounting rate in percentage terms
- n = Time period in years
- m = frequency of compounding or discounting
- g = growth rate in percentage terms
- A = Annuity amount
NOTE:
- Formulas mentioned hereunder presume annual compounding or discounting.
- In case of intra-year compounding or discounting, rate has to be divided by frequency of compounding (replace r by r/m )and time period has to be multiplied by frequency of compounding (replace n by n x m)
- Formulas for annuity presume a regular (ordinary or deferred) annuity wherein, the cash flows occur at the end of the period. In case of annuity due (cash flow occurs at the beginning of the period), the formula is as under.
- Value of Annuity Due = (value of regular annuity) x (1+ r)